Ds04
DS04
통계적 데이터 분석
1. 기초 확률론
확률 실험 (random experiment)
- 결과가 확률적으로 달라질 수 있는 실험
- 예: 주사위 던지기, 동전 던지기
표본 공간 (sample space)
- 가능한 모든 확률 실험 결과(outcome)들의 집합
- 예: S = 1,2,3,4,5,6 , S = {H, T}
사건 (event)
- 특정 조건을 만족하는 결과들로 구성된 부분집합
- 예: E = 1,3,5 , E = {H}
확률 공리 (axioms of probability)
- 모든 사건 E에 대해 P(E)를 사건 E가 발생할 확률이라 부른다.
- Axiom 1: 모든 확률은 0에서 1 사이의 값을 갖는다. (예: P 1 = ⋯ = P 6 = 1/6)
- Axiom 2: 전체 표본 공간에 대한 확률은 1이다. (예: P 1, … , 6 = 1)
-
Axiom 3: 상호배반적인 E1, … , En에 대해 다음이 성립한다.
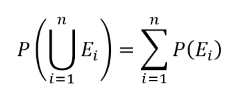
확률 변수 (random variable, 줄여서 r.v.)
- 확률 실험에 의한 각 결과를 수치적 값으로 대응시키는 함수
확률 함수 (probability function)
- 확률 변수 X가 특정 값을 가질 때의 확률은 다음과 같이 표기한다.
- P(X = a) or PX(a)
확률 분포 (probability distribution)
- 확률 변수가 어떤 값을 가질지에 대한 확률에 대한 분포
결합 확률 분포 (joint-)
- 확률 변수가 둘 이상인 경우에 대해 정의된 확률 분포
- 두 개의 확률 변수 X, Y에 대해 다음과 같이 표기한다.
- P(X = a, Y = b) or PX,Y(a, b)
주변 확률 분포 (marginal-)
- 확률 변수가 둘 이상인 경우 특정 변수에 대한 확률 분포
- 예: Val Y = 확률 변수 Y가 가질 수 있는 모든 값의 집합
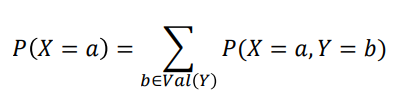
이산형 분포 (discrete distribution)
- 확률 변수가 취할 수 있는 값이 이산적인 경우의 분포
연속형 분포 (continuous distribution)
- 확률 변수가 취할 수 있는 값이 연속적인 경우의 분포
누적 분포 함수 (cumulative distribution)
- 확률 변수가 특정 값보다 작거나 같은 값을 취할 확률을 나타내는 함수
확률 밀도 함수 (probability density function)
- 확률 변수의 밀도를 나타내는 함수
적률 (moment)
- 확률 변수의 특정 함수값을 구하는 것
기대값 (expectation)
- 확률 변수의 평균값
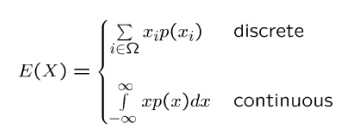
분산 (variance)
- 확률 변수의 흩어진 정도를 나타내는 값
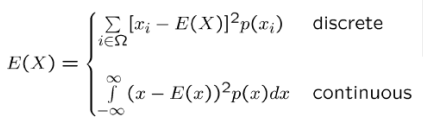
균등 분포 (uniform distribution)
- 모든 값들이 동일한 확률로 나타나는 분포
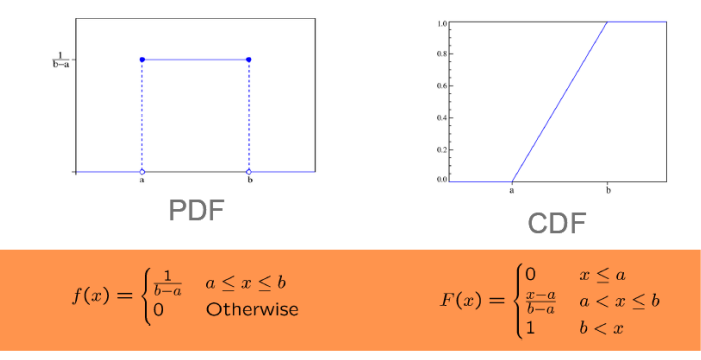
다항 정규 분포 (multivariate Gaussian distribution)
- 다항 정규 분포는 다항 분포에서 각각의 카테고리가 정규 분포를 따르는 경우를 말한다. 다항 분포는 여러 개의 값을 가질 수 있는 독립 확률변수들에 대한 확률분포를 가리키며, 각 시행에서 발생 가능한 결과가 k가지로, 각 독립적인 시행에서 i번째 결과 확률은 p_i로 고정시키는 것이다.
조건부 확률 (conditional probability)
- 사건 A가 발생했을 때 사건 B가 발생할 확률을 다음과 같이 정의한다.
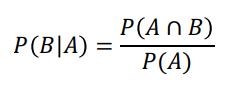
독립 (independence)
- 다음이 성립하면 확률 변수 X와 Y가 독립이라고 한다.
-
P(X) = P(X Y) - 이는 다음과 동치이다.
- P(X, Y) = P(X)P(Y)
조건부 독립 (conditional independence)
- 다음이 성립하면 주어진 Z에 대해 X가 Y에 조건부 독립이라고 한다.
-
P(X) = P(X Y, Z) - 이는 다음과 동치이다.
-
P(X, Y Z) = P(X Z)P(Y Z)
연쇄 법칙 (chain rule)
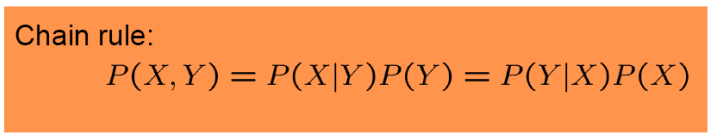
베이즈 법칙 (Bayes rule)
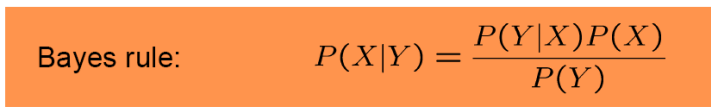
2. MLE와 MAP
MLE(Maximum Likelihood Estimation) : 최우도측정
최우도 추정은 확률 분포에서 (데이터를 이용해) 가능성을 최대화하는 모수를 추정하는 방법이다. 즉, 가장 가능성이 높은 모수를 찾는 것이다. 최우도 추정은 표본의 수가 충분히 클 때 바람직한 통계적 속성(일치성, 최량 점진적 정규성)을 갖는다. 최우도 추정은 점추정치를 구하기 위해 가장 많이 사용하는 방법 중 하나이다.


MAP(Maximum A Posteriori) : 최대사후확률
사전 분포(prior distribution)와 가능도 함수(likelihood function)를 곱한 값의 최댓값을 찾는 것이다. 최대 사후 추정은 매개 변수에 대한 사전 정보가 있을 때 사용한다. MLE와 달리 MAP는 매개 변수와 관련된 사전 지식을 고려한다.

MLE vs MAP
MLE는 매개 변수에 대한 사전 정보가 없을 때 사용하고 MAP는 매개 변수에 대한 사전 정보가 있을 때 사용한다. MLE는 매개 변수에 대한 관측 확률만 고려하고 매개 변수와 관련된 사전 지식을 고려하지 않는다. 반면 MAP는 사전 지식(보통 매개 변수의 도메인 지식에 의해 정보화된)이 포인트 추정치를 효과적으로 규제한다.
3. 가설 검정
가설 검정 (hypothesis testing)
- 아직 밝혀지지 않은 가설을 검사하여 옳고 그름을 판정
가설 (hypothesis)
- 하나 또는 그 이상의 모집단(population)에 대한 기술
- 모집단 특성에 대한 모수(parameter)로 표현됨
- 귀무가설과 대립가설로 나뉨
- 귀무가설(null-): 일반적으로 가정하고 있는 가설 (예: 𝐻0: 𝜇𝐴 = 𝜇𝐵)
- 대립가설(alternative-): 대립되는 가설 (예: 𝐻1: 𝜇𝐴 ≠ 𝜇𝐵 또는 𝐻1: 𝜇𝐴 < 𝜇𝐵)
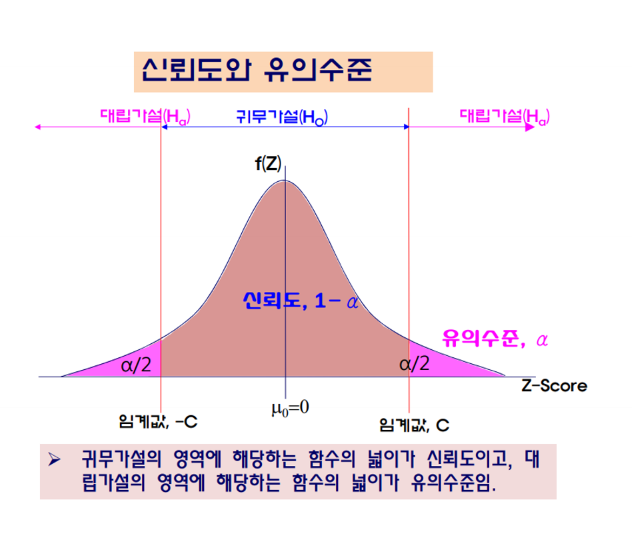
통계적 가설 검정 (statistical hypothesis testing)
- 가설을 설정한 후 검정통계량과 유의수준(significance level)에 따라
- 귀무가설을 기각(reject)할지 채택(do not reject)할지 결정
가설 검정 단계
- 귀무가설, 대립가설 설정
- 검정방법에 따른 기각역(rejection region) 설정
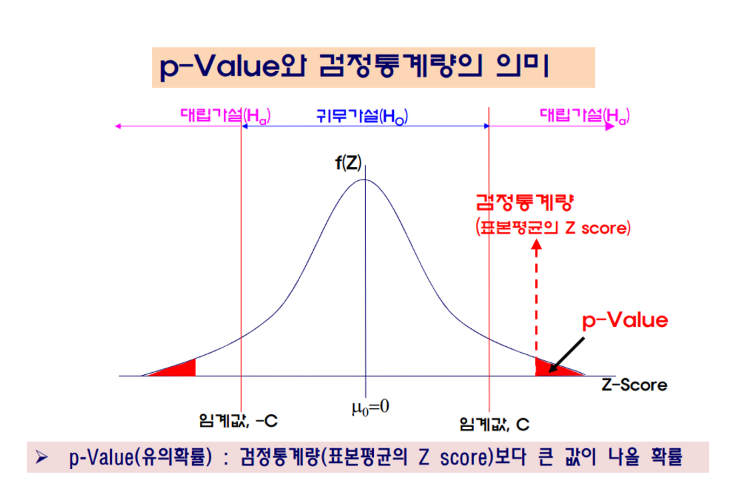
- 검정방법에 따른 검정통계량(test statistic) 계산
- 비교를 통한 귀무가설의 기각/채택 여부 결정
결과해석