Ds05
DS05
회귀(Regression)
지도학습
- 주어진 데이터와 연관된 데이터 사이의 관계를 학습하여 x로부터 y를 예측하는 것
회귀
- 독립 변수 x = (x1, x2, … xp)와 종속 변수사이의 관계 f를 학습
- 최소제곱오차(MSE)를 활용하여 loss를 구한다.
- 모델 타입 : single, multiple linear regression
단순선형회귀
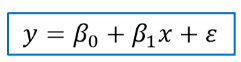
- 최소제곱추정(OLS estimate) : 오차제곱합을 최소로하는
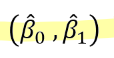
- 오차제곱합(SSE) :
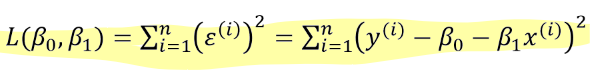
- SSE : 에러의 분포, 0에 가까울수록 회귀모델이 좋다.
- SSR : 회귀값, 0에 가가울수록 회귀모델이 안좋다.
- SST : 전체 데이터
다중선형회귀
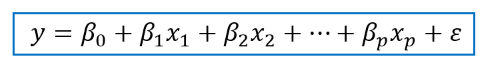
단순선형회귀의 확장
수정된 결정계수
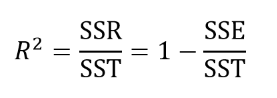
수정된 결정계수는 독립변수의 개수가 많아짐에 따라 무조건 증가하는 결정계수의 문제점을 보완한 통계량으로 회귀 모형에 적합하지 않은 변수를 투입 시 이에 대한 Penalty를 부여하는 것을 특징이다.
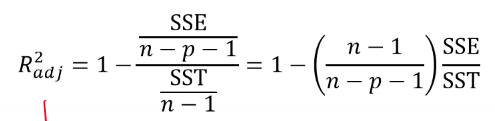
수정된 결정계수가 결정계수보다 10% 이상 차이가 나면 모형에 문제(ex: 과적합)가 있음을 의심해야 한다.

적합도
- 결정계수
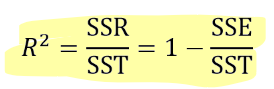
R2이 1에 가까울수록 종속변수의 총 변동성이 회귀모델에 의해 잘 설명된다고 해석 가능
- 피어슨 상관계수
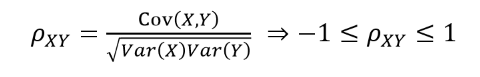
1에 가까울수록 양의 선형상관관계 -1에 가까울수록 음의 선형상관관계
- 표본상관계수
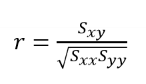
선형회귀분석의 결정계수가 표본상관계수의 제곱과 같다.
성능평가
MSE(Mean Squared Error)

MAE(Mean Absolute Error)
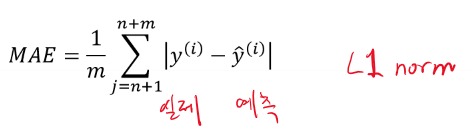
MAPE(Mean Absolute Percentage Mean)
MAE를 0에서 100사이의 값으로 나타낸 것
분류(Classification)
- 주어진 데이터 레코드들에 대해 다른 속성들로부터 클래스 속성을 예측할 수 있는 모델 학습
학습 성능 평가
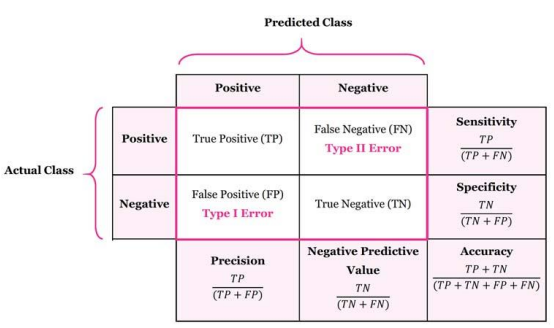
- Precision = TP / ( TP + FP )
- Recall = TP / ( TP + FN )
- F1 score = 2 / ( ( 1 / Precision ) + (1 / Recall) )
- ROC 커브 : TPR vs FPR의 그래프(tradeoff 관계)
- AUC(area under curve): 1에 가까울수록 우수
- 교차 검증(cross validation) : 초기 훈련 데이터에 너무 의존적이지 않은 모델 학습 필요
- k-fold 교차 검증: 훈련 데이터를 k개로 나눠서, 1개를 나머지 k-1개로 훈련하는 평가를 k번 반복
분류 기법
의사 결정 나무
- 트리 모델 학습을 위해 최적 분리(split) 탐색
- 분리 기준 : 불순도 평가
- 불순도 평가 : 지니 계수, 엔트로피 등
- 비교적 단순하지만 직관적이고 해석이 쉬움.
가우시안 나이브 베이즈
- 나이브 베이즈: 속성들은 클래스에 조건부 독립으로 가정
- 모수(parameter) 추정을 통한 통계적 분포 학습
서포트 벡터 머신
- 분류의 마진(margin)을 최대로 하는 결정 경계(decision boundary) 탐색
- 선형 분리가 불가능한 경우, 여유(slack) 변수를 도입한 소프트 마진 최적화 문제를 통해 해결
- 커널 트릭을 활용하여 특징 공간의 차원을 높여 선형 분리 문제 등 더 쉬운 문제로 해결하기도 함.