Dl02

DL02

Optimization

• 에러함수 J(x)의 최솟값을 찾는다.

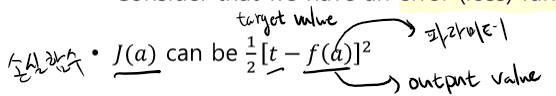
Gradient descent

• 기울기를 관찰하여 기울기의 반대방향으로 최솟값이 될 때까지 이동한다.
• Local optimum : 다항 함수에서의 지역 최저점, 전역 최저점이 아닌 지점
• 차원이 올라간다면 전역 최저점을 찾는 것의 불가능

Convex optimization

• Convex function에서 최저값을 찾는 것, 수학적 계산 방법으로 gd와는 다르다.

Convex relaxation

• Convex function이 아닌 다항함수를 Convex function 형태로 변환해주는 것!
• Convex relaxation을 진행하여 Convex optimization을 사용하여 나온 최저값이 원 함수의 최저값과 비슷하다!

Constrained optimization

• 특정 지점에서의 최솟값을 구하는 방법
• Karush-Kuhn-Tucker(KKT) 방법을 이용하여 구할 수 있다.

ML Definition

• training data를 이용하여 학습한 뒤 비슷한 유형의 데이터의 패턴을 일반화하는 기법

Definition

• 데이터를 사용하여 T를 수행할 때 P를 향상 시킨다.
• E(Experience) : 데이터
• T(Task) : 패턴을 일반화 하는 작업
• P(Performance) : 성능

Task, T

• Supervised learning
  • Classification
  • Regression
• Unsupervised learning
  • Clustering
• Reinforcement learning

Performance, P

• 머신러닝 알고리즘의 정량적 성능
• Classification
  • Accuracy
  • Error rate
  • Average log-probability
• Regression
  • Mean Square Error(MSE)
  • Root Mean Square Error(RMSE)
  • R square
• Anomaly detection : 이상치 검출
  • Recall(재현율)
  • Precision(정확도)

Experience, E

• 전체 데이터셋
• Supervised Learning
  • 모든 샘플에 labeling이 되어 있다.
• Unsupervised Learning
  • 샘플에 labeling이 되어 있지 않다.
• Semi-supervised Learning
  • 부분 샘플에 labeling이 되어 있다.

Linear Regression

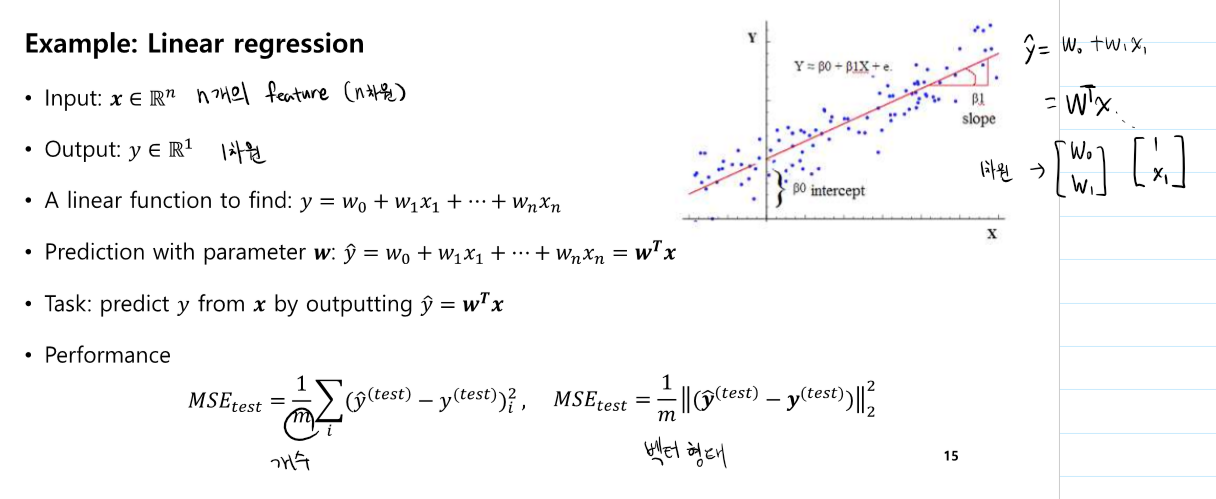
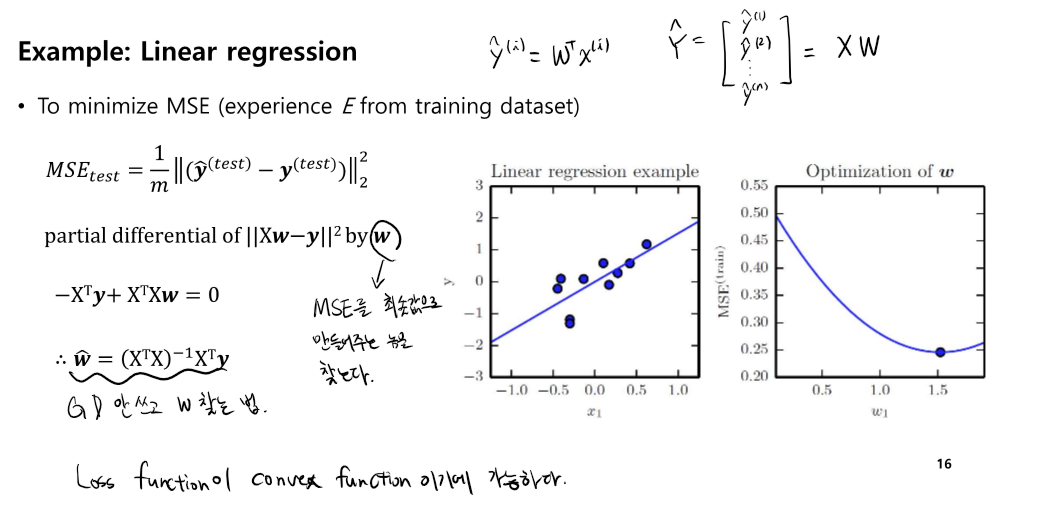
• gd를 안쓰고 w를 찾는 것이 가능하다.(loss function이 convex 형태일 때)

Modal Capacity

• Training Performance : 트레이닝 데이터에 대한 분류 성능
• Test Performance : 트레이닝 데이터로 학습시킨 모델을 이용하여 test 데이터에 대한 분류를 진행하였을 때의 성능
• test 데이터가 독립적으로 생성되었고 동일한 분포를 갖는다면 training 데이터를 학습시켰을 때 실제 데이터에 대해서도 좋은 성능을 낼 것이다.
• 고차원으로 갈 수록 capacity가 높다. 복잡한 특징을 일반화할 수 있다.
• capacity가 너무 낮아지면 underfitting이 일어나고 너무 높아지면 overfitting이 일어난다.

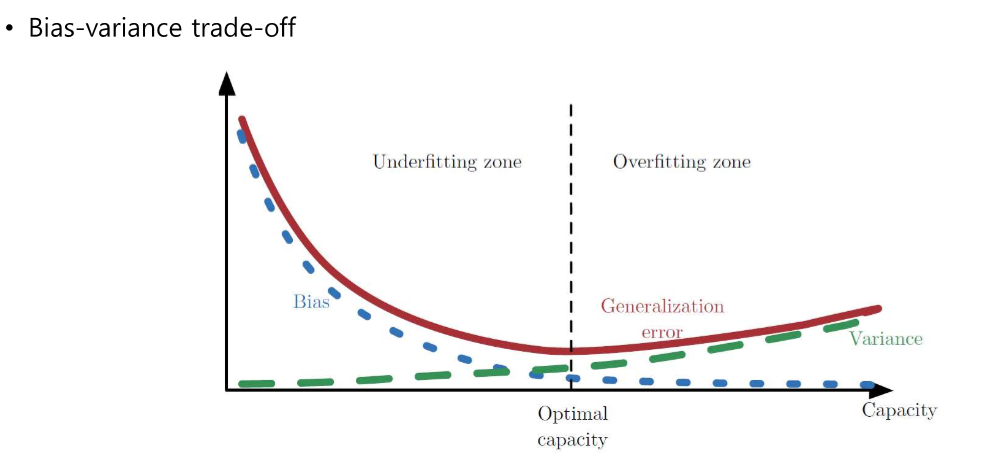
일반화 성능

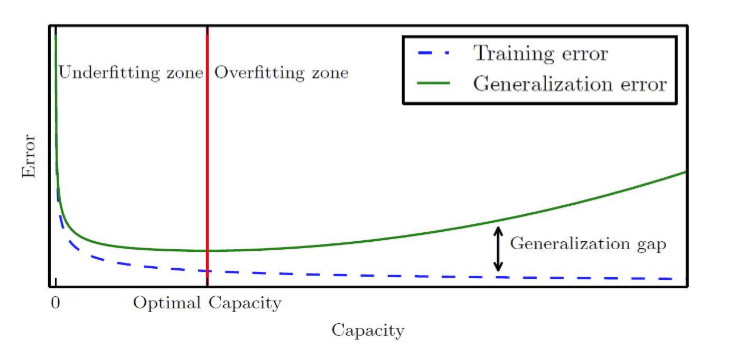
• 데이터 셋이 많으면 높은 optimal capacity를 가지고 데이터셋이 적으면 적은 optimal capacity를 가진다.
• 위 그림에서 빨간 선이 optimal capacity 구간이다.

정칙화

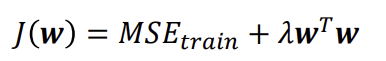
• overfitting을 방지하기 위한 장치

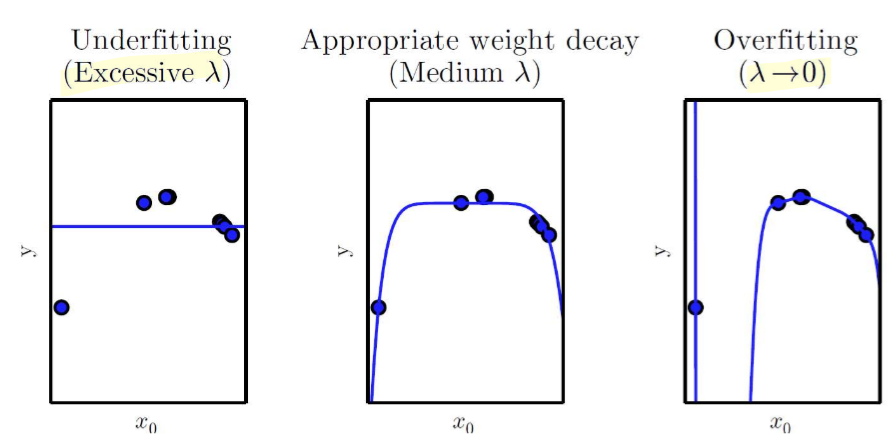
이때 λ가 너무 커지면 capacity가 낮아지고 underfitting이 될 수 있고 λ가 너무 작아지면 capacity가 커지고 overfitting이 될 수 있다.

Hyperparameters and Validation Sets

• hyperparameter란 model capacity를 결정하기 위한 요소이다.
• validation set이란 training data에서 일부 validation data를 뽑아내어 검증하기 위해 사용되는 데이터 셋이다.
• k-fold cross validation : training 데이터셋을 n개로 쪼갠 후 n-1개의 데이터를 이용하여 학습하고 나머지 1개의 데이터를 이용하여 검증하는 과정을 k번 진행하는 기법이다.

Estimators

• Point estimation : 정추정(theta(실제값)를 theta hat(추정값)으로 추정한다.)
• Bias : theta와 theta hat의 차이
• Variance : theta hat이 얼마나 넓게 잘 분포되어 있는지를 알려주는 theta hat의 분산

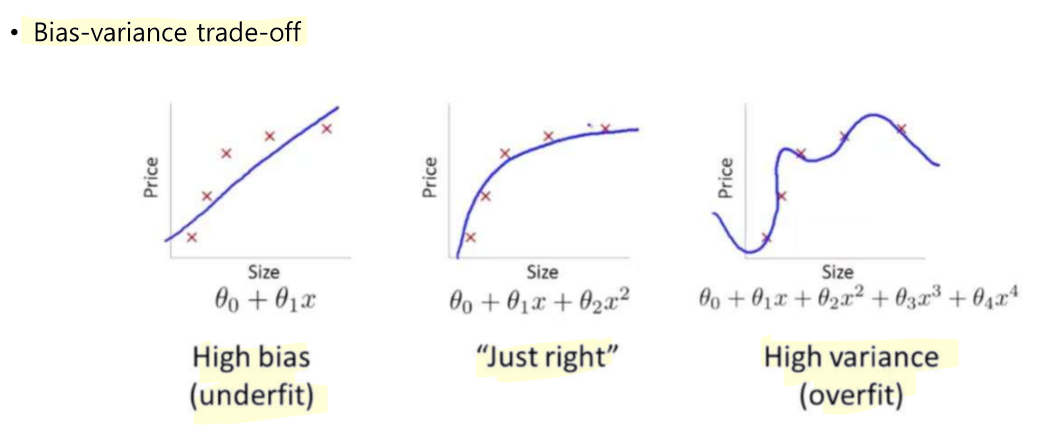
• bias가 너무 높아지면 underfitting이 일어나고 variance가 너무 높아지면 overfitting이 일어난다.

MAP Estimator vs ML Estimator

• 각각의 개념
• 차이점

Maximum Likelihood Estimation

• 데이터 분포를 추정하는 문제

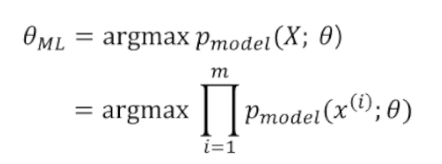
• 위 식은 어떤 파라미터 세타를 가졌을 때 데이터 x가 생성될 확률을 가지는 P 모델 중에서 확률이 가장 높은 모델을 생성해내는 세타가 Maximum likelihood Estimator이다.

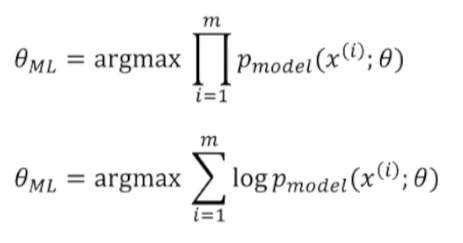
• 최댓값을 찾을 때 확률의 곱셈은 로그의 덧셈으로 찾을 수 있다.

Bayesian Statistics

• frequentist
  • 세타는 고정되어 있다는 전제하에 추정하는 것이다.
• Bayesian
  • 세타가 고정되어 있지 않고 어떤 확률분포를 따른다는 전제하에 추정하는 것이다.

X가 주어졌을 때 세타를 찾는 Bayesian 확률 식이다.

Stochastic Gradient Descent

• 트레이닝 데이터를 작은 집합으로 나누어서 각 집합을 미니배치라 칭하고 해당 미니배치만을 이용해서 gradient descent 기법을 이용하여 최솟값을 찾는 과정을 전체 데이터에 대하여 진행하는 방법이다. 모든 미니배치 데이터들에 대하여 연산이 진행되면 그것을 1 epoch라고 하고 이러한 epoch를 여러 번 돌려서 최적의 결괏값을 찾을 수 있다.